한국외대 '신찬수' 교수님과 '쉬운 코드'님의 강의 자료를 참고하였습니다.
개념을 공부하고, 시뮬레이터를 활용하여 노드의 동작 원리를 이해한다.
하단의 링크는 rbtree visualization을 확인할 수 있는 링크이다. 참고하여 학습을 진행한다.
https://www.cs.usfca.edu/~galles/visualization/RedBlack.html
Red/Black Tree Visualization
www.cs.usfca.edu
#1 레드블랙 트리 기본 개념과 특징
1. 레드블랙 트리 개념
1. 이진 탐색 트리(BST)의 한 종류
2. 스스로 균형 잡는 트리
3. BST의 worst case의 단점을 개선 : worst case = 한 방향으로 편향된 이진탐색 트리 > O(N)
4. 모든 노드는 red 혹은 black
위 3번 특징을 개선하기 위해서 2번 특징이 존재.
최악의 경우에도 O(logN).
2. red-black 트리 속성
1. 모든 노드는 red 혹은 black
2. 루트 노드는 black
3. 모든 nil(leaf) 노드는 black
4. red의 자녀들은 black or red가 연속적으로 존재할 수 없다.
5. 임의의 노드에서 자손 nil 노드들까지 가는 경로들의 black 수는 같다.
(자기 자신은 카운트에서 제외)
nil 노드란?
- 존재하지 않음(NULL)을 의미하는 노드
- 자녀가 없을 떄 자녀를 nill 노드로 표기
- 값이 있는 노드와 동등하게 취급
- RB트리에서 leaf 노드는 nil 노드
#5 속성에서 나오는 새로운 개념 : 노드 x의 black height
- 노드 x에서 임의의 자손 nil 노드까지 내려가는 경로에서의 black 수
(자기 자신은 카운트에서 제외)
- #5 속성을 만족해야 성립하는 개념
색을 바꾸면서도 #5 속성 유지하기
RB 트리가 #5 속성을 만족하고 있고 두 자녀가 같은 색깔을 가질 때
부모와 두 자녀의 색을 바꿔줘도 #5 속성은 여전히 만족한다.
(나중에 삽입 및 삭제에 사용되는 개념)
3. RB 트리는 어떻게 균형을 잡는가?
삽입/삭제 시 주로 #4, #5를 위반한다.
이를 해결하려고 구조를 바꾸다 보면 자연스럽게 트리의 균형이 잡히게 된다.
#2 레드블랙 트리의 삽입 방식
0. 삽입 전 RB 트리 속정 만족한 상태
1. 삽입 방식은 일반적인 BST와 동일
2. 삽입 후 RB 트리 위반 여부 확인
3. RB 트리 속성을 위반했다면 재조정
4. RB 트리 속성을 다시 만족
1. 삽입 과정
삽입하는 노드의 색은 항상 red
2. 삽입 후 #4 속성 위반 case.3
insert(50)
- 두 nil 노드의 색은 black으로 고정한다. #3 속성 만족
- 만약 루트노드라면 현재 상태가 #2 속성을 위반한 상태 > 루트 노드를 black으로 바꿔준다.
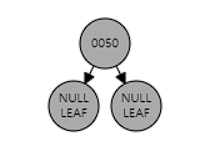
insert(20)
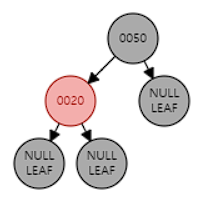
왜 새로 삽입하는 노드는 red인가?
- 삽입 후에도 #5 속성을 만족하기 위해
insert(10)

- #4 속성 위반 해결 방법
- red가 한 쪽으로 몰려 있으니 red하나를 반대편으로 옮겨 준다면?
*구조를 바꿔준 뒤에 BST의 특징 도한 유지되어야 한다.
- 구조를 바꾸면서도 BST의 특징을 유지시키는 방법은 회전이다.
'50과 20의 색깔을 바꿔준 다음 회전을 시켜도 되고, 회전을 시킨 다음에 색깔을 바꿔도 된다.'
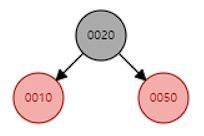
조건
(1) 삽입된 red 노드가 부모의 왼쪽* 자녀
(2) 부모도 red고 할아버지의 왼쪽* 자녀
(3) 삼촌(=부모의 형제)은 black
즉, '선형의 노드 형태'일 때 성립하는 case.3이다.
해결방법
부모와 할아버지의 색을 바꾼 후 할아버지 기준으로 오른쪽*으로 회전한다.
* 오른쪽 왼족 바꿔도 성립
3. 삽입 후 #4 속성 위반 case.2
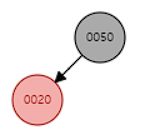
insert(40)
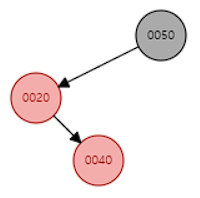
위 경우와 다르게 이러한 형태는 자식과 부모, 할아버지 노드가 꺾여있는 것을 확인할 수 있다.
1. 20을 기준으로 왼족으로 회전한다.
회전 후에도 #4 외의 속성들을 만족하며 이제 case.3의 형태가 된다.

2. 40과 50의 색을 바꾼다.
3. 50을 기준으로 오른족으로 회전한다.

조건
(1) 삽입된 red 노드가 부모의 오른쪽* 자녀
(2) 부모도 red고 할아버지의 왼쪽* 자녀
(3) 삼촌(=부모의 형제)은 black
즉, '선형의 노드 형태'일 때 성립하는 case.2이다.
해결방법
부모를 기준으로 왼쪽*으로 회전한 뒤 case.3의 방식으로 해결
* 오른쪽 왼족 바꿔도 성립
4. 삽입 후 #4 속성 위반 case.1

insert(30)

red가 한쪽으로 몰려있지 않아서(=삼촌 red) 옮길 수가 없다.


20이 루트 노드라서 #2 속성을 위반한다.
20을 black으로 바꿔준다.

조건
(1) 삽입된 red 노드의 부모 red
(2) 삼촌(=부모의 형제)은 red
즉, 부모와 삼촌 노드의 색깔이 red일 때 성립하는 case.1이다.
해결방법
부모와 삼촌을 black으로 바꾸고 할아버지를 red로 바꾼뒤 할아버지에서 다시 확인을시작한다.
🤔 할아버지가 루트노드인 경우, 할아버지의 부모노드가 red일 경우 등 다시 확인 필요.
#3 레드블렉 트리 삽입 예제
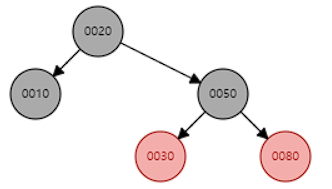
insert(40) - case.2 발생


insert(35) - case.2 발생
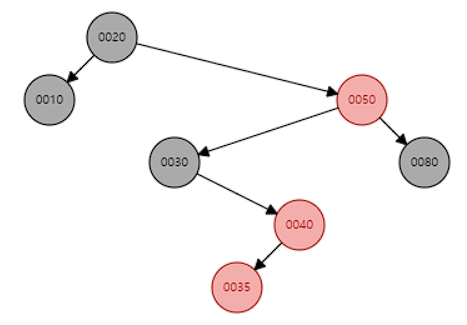
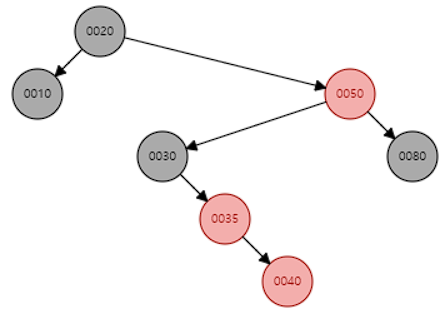

insert(25) - case.1 / case.2 / case.3

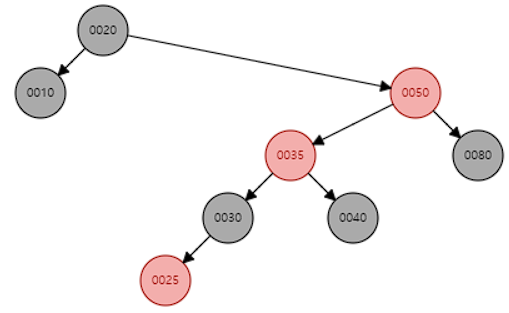
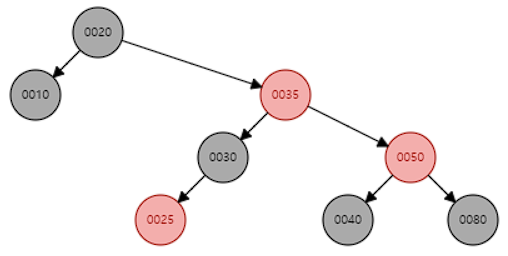

글을 마치며,
처음 rbtree를 마주했을 때는 이해가 잘 안됐는데, 시뮬레이터를 활용하여 학습하니 도움이 됐다.
해당 주소를 알려준 Mr.한에게 감사를 표한다.
다음 포스팅에서는 rbtree의 삭제에 대해 학습한다.
긴 글 읽어주셔서 감사드립니다.
22.11.26
'TIL (Today I Learned) > 알고리즘' 카테고리의 다른 글
| [알고리즘] Big O (1) | 2023.03.16 |
|---|---|
| [알고리즘] RB Tree삭제 동작 원리 #2 (0) | 2022.11.26 |


댓글