[알고리즘] Big O

#1 Big O

 

Big O는 코드가 얼마나 효율적으로 실행되는지 수학적으로 비교하는 방법.

 

동일한 작동을 하는 코드 A와 코드 B가 있다고 생각해 보자.

코드 A는 15초 동안 실행되고, 코드 B는 1분 동안 실행 된다면, 우리는 코드 A가 더 낫다고 생각할 것이다.

이것이 시간 복잡도이다.

하지만, 시간 복잡도는 시간으로 측정하지 않는다.

무슨 소리예요, 방금 15초와 1분을 비교했잖아요? 하실 것이다.

왜냐면 방금 시간을 측정한 컴퓨터보다 성능이 더 좋은 컴퓨터로 B코드를 실행하면 15초보다 빠르게 실행될 수도 있기 때문이다. 따라서, 무언가를 완료하는 데 걸리는 작업 수로 측정하는 것이 더욱 정확하다.

 

시간 복잡도 외에도 공간 복잡도를 측정해야 한다.

코드 A는 매우 빠르게 실행되지만 상대적으로 실행할 때 많은 메모리를 차지한다(가정).

코드 B는 완료하는 데 훨씬 더 오래 걸리지만 메로리를 덜 차지할 수 있다(가정).

 

메모리 공간을 보존하는 것이 가장 중요한 우선순위이고 추가시간을 가져도 괜찮다면 코드 B가 더 나을 수도 있다.

 

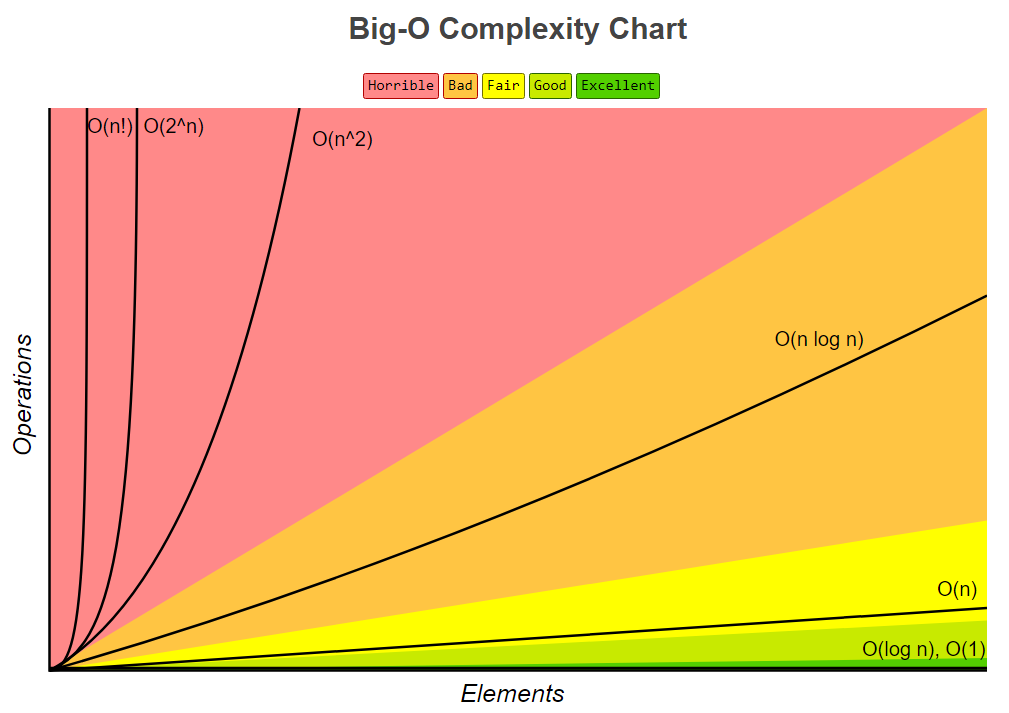
시간 복잡성 및 공간 복잡성을 다룰 때 크게 Omega, Theta, Omicron을 이야기한다.

최선의 시나리오는 단 한 번에 일을 수행하는 것으로 Omega, 최악의 시나리오는 가장 작업이 많은 경우인 Omicron, 일반적으로 평균적인 작업 수를 Theta라고 말한다.

Big O에서 O는 Omicron으로 최악의 경우에 대해 이야기하는 것이다.

 

 

#2 O(n)

n번 작업하는 코드

def solution(n):
	for i in range(n):
    	print(i)

단순화를 위해서 O(2n)의 경우에도 O(n)이라고 표기한다.

 

 

#3 O(n^2)

n^2번 작업하는 코드

def solution(n):
	for i in range(n):
            for j in range(n):
                print(i, j)

만약 n^3번 작업하는 코드라고 해도 단순화를 위해서 O(n^2)이라고 표기한다.

또한, O(n^2 + n)와 같은 경우에는 n의 값이 커질수록 '+ n'의 영향이 약해지기 때문에 O(n^2)이라고 표기한다.

 

 

#4 O(1)

단 한번 작업하는 코드

def solution(n):
	return n + n

상수시간이라고도 하며, n이 증가함에 따라 작업 횟수는 일정하게 유지된다.

 

 

#5 O(log n)

log n의 시간 복잡도를 가지기 위해서는 우선 정렬된 리스트가 필요하다.

해당 리스트를 탐색할 때 중간을 기준으로 반으로 나눠서 탐색하면 최악의 경우 log n번 반복하면 탐색을 완료할 수 있다.

log n은 상수시간만큼은 아니지만 O(n) 또는 O(n^2) 보다 훨씬 효율적이다.

 

이 외에도 O(nlog n) - 병합 정렬과 퀵 정렬 - 이 있다. 주로 다양한 유형의 데이터를 정렬하려는 경우 사용된다 ( 주로 문자열 정렬 )

 

 

그러나, 입력값이 a, b처럼 서로 다른 수라면 시간 복잡도는 O(n)이 아니라 O(a + b)와 같이 표기해야 한다.

 

출처 : https://www.bigocheatsheet.com/

#6 LIST

 

python의 list자료구조에서 append()와 pop()은 O(1)의 시간 복잡도를 가진다.

하지만, insert(0, number)와 pop(0)의 경우 해당 인덱스를 찾고 다른 요소의 인덱스를 재정렬 해야 하기 때문에 O(n)의 시간 복잡도를 가지게 된다.

 

특정 요소를 찾을 때 해당 요소를 찾으려면 O(n)의 시간을 갖게 된다.

하지만 인덱스를 기반으로 찾는다면? O(1)의 시간 복잡도를 가지게 된다. 왜냐하면 인덱스를 기반으로 메모리의 해당 위치로 직접 이동할 수 있기 때문이다.

 

 

#7 마치며

https://www.bigocheatsheet.com/

Big-O Algorithm Complexity Cheat Sheet (Know Thy Complexities!) @ericdrowell

 

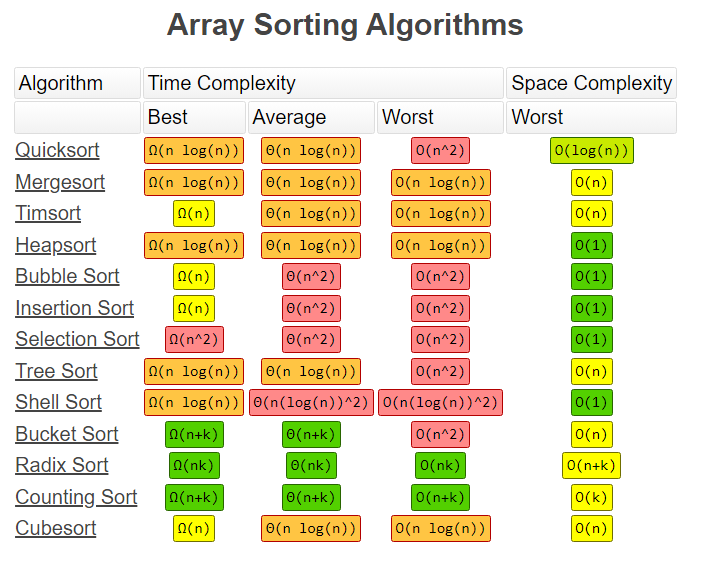
위 사이트에서 볼 수 있듯이 시간 복잡도가 유리하다고 공간 복잡도가 유리한 것은 아니다.

반대로, 상황에 따라 시간 복잡도가 유리한 정렬 알고리즘이 다르다는 것을 유의해야 한다.

위 사이트에 직접 들어가서 확인해 보길 추천한다.